Mặt cầu bán kính r có diện tích là?

Mặt cầu có bán kính r thì có diện tích là:

Công thức tính diện tích mặt cầu bán kính r là S = 4xπx2R

Trong đó:

• S là diện tích
• π là 3.14159265359
• R là bán kính

Hình cầu là gì?

Xem thêm: Máy cưa vòng cắt sắt

Trong toán học, quả cầu (hay còn gọi là khối cầu, hình cầu, bóng hay bong bóng) thể hiện phần bên trong của một mặt cầu; cả hai khái niệm quả cầu và mặt cầu không chỉ được dùng trong không gian ba chiều mà còn cho cả các không gian có số chiều ít hơn hay nhiều hơn, và tổng quát là cho các không gian metric.

Tùy theo đối tượng nghiên cứu, người ta có thể cứu xét quả cầu là phần tính luôn các điểm biên (như khái niệm quả cầu trong hình học cổ điển và khái niệm hình cầu đóng trong tô pô) hay ngược lại khối cầu là “phần bên trong” không kể các điểm biên (như khái niệm hình cầu mở trong tô pô).

Đặc biệt trong tô pô học, ngành toán học phát triển nhất hiện nay, khái niệm quả cầu trong nhiều trường hợp chỉ có tính cách biểu trưng cho một lớp đối tượng thỏa mãn cùng một đặc tính vì các hình khối đơn giản như hình quả trám, hình lập phương thậm chí hình cái ly không quai đều được xem là các khối cầu.

Chu vi hình tròn là gì?

Xem thêm: Khí thiên nhiên là gì?

Chu vi hình tròn hay độ dài đường tròn là đường biên giới hạn của hình tròn. Công thức của chu vi hình tròn là lấy đường kính nhân với pi hay 2 lần bán kính nhân pi

Công thức tính chu vi hình tròn:

C=2R. π hay C=D. π

Trong đó:

• C: là chu vi đường tròn
• D: là đường kính
• R: là bán kính
• π: là hằng số giá trị tương đương 3,14

Quả cầu trong không gian metric

Giả sử M là một không gian metric. Một quả cầu (mở) với bán kính r > 0 và tâm là điểm p trong M được định nghĩa là

{displaystyle B_{r}(p)={xin Mmid d(x,p)<r},}

với d là khoảng cách hay còn gọi là metric. Nếu ký hiệu nhỏ hơn (<) trong định nghĩa trên được thay

bằng ký hiệu nhỏ hơn hoặc bằng (≤), ta được định nghĩa về cái gọi là quả cầu đóng:

{displaystyle {bar {B}}_{r}(p)={xin Mmid d(x,p)leq r}}

Chú ý rằng, bất kể là đóng hay mở, quả cầu luôn luôn chứa điểm p vì r>0. Một quả cầu đơn vị (đóng hay mở) là quả cầu có bán kính r bằng một trong hai định nghĩa nói trên.

Một tập con của một không gian metric được gọi là bị chặn nếu nó được chứa trong một quả cầu nào

đó. Một tập hợp được gọi là bị chặn toàn phần nếu cho trước một bán kính r bất kỳ, có thể tìm được

một số hữu hạn quả cầu có bán kính r mà phủ được tập hợp đó.

Các quả cầu mở với metric d tạo ra một cơ sở của topo cảm ứng bởi d (theo định nghĩa). Điều này có

nghĩa là, tất cả các tập mở trong một không gian metric đều có thể biểu diễn bằng hợp của một số quả

cầu mở nào đó.

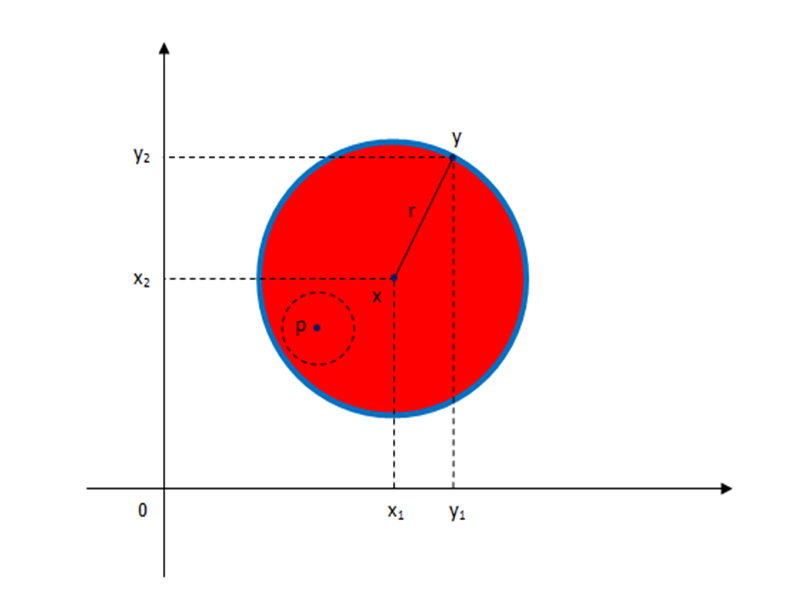
Quả cầu Euclide

Trong không gian Euclide n chiều, với metric thông thường; nếu không gian này là một đường thẳng thì quả cầu mở là một khoảng; và nếu không gian này là một mặt phẳng, thì quả cầu mở là hình đĩa bên trong đường tròn. Một quả cầu đơn vị đóng thường được ký hiệu bằng Dn; phần bên ngoài của quả cầu này là một mặt cầu n-1, được ký hiệu là Sn-1. Chẳng hạn như mặt cầu 3-chiều S3 sẽ là “phần bên ngoài” (hay phần biên) của D4. Hai khái niệm quả cầu và mặt cầu trong không gian có số chiều cao hơn thường được gọi là siêu cầu và siêu mặt cầu. Có thể xem thêm về khái niệm “thể tích” và “diện tích” trong trường hợp không gian có số chiều lớn hơn 3.

Với các metric khác nhau, hình dạng quả cầu trong cùng một không gian có thể khác nhau. Ví dụ:

Trong không gian 2 chiều:

Với chuẩn-1 (tức là theo hình học taxicab), quả cầu là một hình vuông có các đường chéo song song với các trục tọa độ.

Với chuẩn cảm ứng từ khoảng cách Chebyshev, quả cầu là một hình vuông có các cạnh song song với các trục tọa độ.

Trong không gian 3 chiều:

Với chuẩn-1, quả cầu là một bát diện đều với các đường chéo thân song song với các trục tọa độ.

Với chuẩn cảm ứng từ khoảng cách Chebyshev, quả cầu là một khối lập phương có các cạnh song song với các trục tọa độ.